Regla de Kirchhoff de las tensiones

Ley de tensiones de Kirchhoff

Esta ley es llamada también segunda ley de Kirchhoff, ley de lazos de Kirchhoff o ley de mallas de Kirchhoff

La ley de las mallas de Kirchhoff nos dice que:

En un lazo cerrado, la suma de todas las caídas de tensión es igual a la tensión total suministrada. De forma equivalente, la suma algebraica de las diferencias de potencial eléctrico en un lazo es igual a cero.
$\sum_{k=1}^n V_k = V_1 + V_2 + V_3\dots + V_n = 0$

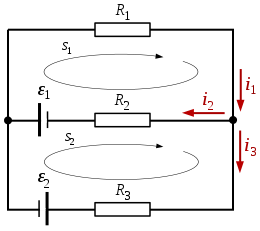
Caso práctico

Asumiendo una red eléctrica consistente en dos fuentes y tres resistencias, disponemos la siguiente resolución:

De acuerdo con la primera ley de Kirchhoff (ley de los nodos), tenemos:

i_1 - i_2 - i_3 = 0 \,

La segunda ley de Kirchhoff (ley de las mallas), aplicada a la malla según el circuito cerrado s1, nos hace obtener:

R_2 i_2 - \epsilon_1 + R_1 i_1 = 0

La segunda ley de Kirchhoff (ley de las mallas), aplicada a la malla según el circuito cerrado s2, por su parte:

R_3 i_3 + \epsilon_2 + \epsilon_1 - R_2 i_2 = 0

Debido a lo anterior, se nos plantea un sistema de ecuaciones con las incógnitas $i_1, i_2, i_3$ :

\begin{cases}<br /><br /><br /> i_1 - i_2 - i_3 & = 0 \\<br /><br /><br /> R_2 i_2 - \epsilon_1 + R_1 i_1 & = 0 \\<br /><br /><br /> R_3 i_3 + \epsilon_2 + \epsilon_1 - R_2 i_2 & = 0 \\<br /><br /><br /> \end{cases}<br /><br /><br />

Dadas las magnitudes:

<br /><br /><br /> R_1 = 100,\ R_2 = 200,\ R_3 = 300,\ \epsilon_1 = 3,\ \epsilon_2 = 4<br /><br /><br />

la solución definitiva sería:

\begin{cases}<br /><br /><br /> i_1 = \frac {1} {1100} \\<br /><br /><br /> i_2 = \frac {4} {275} \\<br /><br /><br /> i_3 = - \frac {3} {220} \\<br /><br /><br /> \end{cases}<br /><br /><br />

Se puede observar que $i_3$ tiene signo negativo, lo cual significa que la dirección de $i_3$ es inversa respecto de lo que hemos asumido en un principio (la dirección de $i_3$ -en rojo- definida en la imagen).